Молярна маса речовини ,
де m–маса однорідного тіла (системи); -кількість речовини (число молей) цього тіла (системи). Виражається в одиницях г / моль (або кг / моль).
Одиниця маси, що дорівнює 1/12 маси атома вуглецю 12 C, називається атомної одиницею маси (а.е.м.). Маси атомів або молекул виражені в атомних одиницях маси називають відповідно відносною атомною або відносної молекулярної масою речовини. Відносна молекулярна маса речовини складається з відносних атомних мас хімічних елементів, що становлять молекулу речовини. Відносні атомні маси хімічних елементів наводяться в таблиці Д. І. Менделєєва (див. Також таблицю 8 додатка даного посібника).
Молярна маса речовини чисельно дорівнює відносній атомній або молекулярній масі даної речовини, якщо розмірність а.е.м. замінити на розмірність г / моль.
2.10.5. Встановлення формули хімічної сполуки по його елементного складу
Найпростіша хімічна формула речовини визначається на підставі відомих величин масових часток входять до складу цієї речовини елементів.
Припустимо є зразок речовини NaxPyOz масою mo р Розглянемо як визначається його хімічна формула, якщо відомі кількості речовини атомів елементів, їх маси або масові частки у відомій масі речовини. Формула речовини визначається відношенням:
Це ставлення не зміниться, якщо кожен його член розділити на число Авогадро:
Таким чином, для знаходження формули речовини необхідно знати співвідношення між кількостями речовин атомів в одній і тій же масі речовини:
Якщо розділити всі члени останнього рівняння на масу зразка mo, то отримаємо вираз, що дозволяє визначити склад речовини:
Приклад 12. Речовина містить 85,71 мас. % Вуглецю і 14,29 мас. % Водню. Молярна його маса дорівнює 28 г / моль. Визначте найпростішу і справжню хімічні формули цієї речовини.
Рішення. Співвідношення між кількістю атомів в молекулі СхНу визначається діленням масових часток кожного елемента на його атомну масу:
Таким чином найпростіша формула речовини. СН2. Найпростіша формула речовини не завжди збігається з його істинною формулою. В даному випадку формула СН2 не відповідає валентності атома водню. Для знаходження істинної хімічної формули необхідно знати молярну масу даної речовини. В даному прикладі молярна маса речовини дорівнює 28 г / моль. Розділивши 28 на 14 (суму атомних мас, що відповідають формульної одиниці СН2), отримуємо справжнє співвідношення між числом атомів в молекулі:
Отримуємо справжню формулу речовини: С2Н4- етилен.
Замість молярної маси для газоподібних речовин і парів в умові завдання може бути вказана щільність по якомусь газу або по повітрю.
В даному випадку щільність газу по повітрю становить 0,9655. На підставі цієї величини може бути знайдена молярна маса газу:
М = Мвозд Dвозд = 29 0,9655 = 28.
У цьому виразі М. молярна маса газу СхНу, Мвозд. середня молярна маса повітря, Dвозд. щільність газу СхНу по повітрю. Отримана величина молярної маси використовується для визначення істинної формули речовини.
В умові задачі може не вказуватися масова частка одного з елементів. Вона знаходиться відніманням з одиниці (100%) масових часток усіх інших елементів.
Приклад 13. Органічне поєднання містить 38,71 мас. % Вуглецю, 51,61 мас. % Кисню і 9,68 мас. % Водню. Визначити справжню формулу цієї речовини, якщо щільність його парів по кисню становить 1,9375.
Рішення. Розраховуємо співвідношення між кількістю атомів в молекулі СхНyОz:
х: у: z = 38,71 / 12: 9,68 / 1: 51,61 / 16 = 3,226: 9,68: 3,226 = 1: 3: 1.
М = М (O2) D (O2) = 32 1,9375 = 62.
Найпростіша формула речовини СН3О. Сума атомних мас для цієї формульної одиниці складе 12316 = 31. Ділимо 62 на 31 і отримуємо справжнє співвідношення між кількістю атомів в молекулі:
Таким чином, справжня формула речовини С2Н6О2. Ця формула відповідає складу двухатомного спирту. етиленгліколю: СН2 (ОН).СН2 (ОН).
Кількість речовини суміші n газів
або ,
Рівняння Менделєєва. Клапейрона (рівняння стану ідеального газу)
,
де т – маса газу, – молярна маса газу, R – універсальна газова постійна, ν. кількість речовини, Т – термодинамічна температура.
Досвідчені газові закони, які є окремими випадками рівняння Менделєєва. Клапейрона для ізопроцессов:
а) закон Бойля-Маріотта (ізотермічний процес: T= const, m= Const)
або для двох станів газу, позначених цифрами 1 і 2,
,
б) закон Гей-Люссака (изобарических процес: р= const, m= Const)
або для двох станів ,
в) закон Шарля (изохорический процес: V= const, m= Const)
або для двох станів ,
г) об’єднаний газовий закон (m= Const)
або для двох станів.
Під нормальними умовами розуміють тиск po = 1 атм (1,01310 5 Па), температуру 0 ° С (T= 273 K).
Закон Дальтона, який визначає тиск суміші n газів.
,
де pi – парціальні тиску компонентів суміші (i= 1,2,n). Парціальним тиском називається тиск газу, який виробляв би цей газ, якби тільки він один знаходився в посудині, зайнятій сумішшю.
концентрація молекул
,
де N – число молекул, що містяться в даній системі; . щільність речовини в системі; V. обсяг системи. Формула справедлива не тільки для газів, а й для будь-якого агрегатного стану речовини.
Рівняння Ван-дер-Ваальса для реального газу
,
де a і b. коефіцієнти Ван-дер-Ваальса
Для ідеального газу рівняння Ван-дер-Ваальса переходить в рівняння Менделєєва. Клапейрона.
Основне рівняння молекулярно. кінетичної теорії газів
,
де п. середня кінетична енергія поступального руху молекули.
Середня молекулярна маса являє собою умовну величину і відноситься до такого однорідного газу, у якого число молекул і загальна маса рівні числу молекул і масі суміші газів.
Якщо відома величина газової постійної суміші, то
(3-7)
Замінюючи газові постійні R1, R2. Rn їх значеннями з рівняння Клапейрона, отримуємо вираз для середньої молекулярної маси, якщо суміш задана масовими частками:
(3-8)
Якщо суміш задана об’ємними частками, то, як випливає з рівняння (3-6),
оскільки то
(3-9)
Середня молекулярна маса суміші газів дорівнює сумі творів об’ємних часток на молекулярні маси окремих газів, що складають суміш.
Парціальний тиск газу може бути визначено через масові частки з рівняння Клапейрона, якщо відомі основні параметри газу:
(3-10)
Для знаходження парціального тиску кожного газу при завданні суміші об’ємними частками можна скористатися законом Бойля. Маріотта, з якого випливає, що при постійній температурі
(3-11)
Парціальний тиск кожного газу дорівнює добутку загального тиску суміші газів на його об’ємну частку.
Рівнянням (3-11) зазвичай користуються при технічних розрахунках і при випробуваннях теплових установок. Об’ємні частки газів визначають спеціальними апаратами. газоаналізаторами.
Питома ентальпія, т. Е. Ентальпія, віднесена до 1 кг, позначається буквою i і являє собою по визначенню складну функцію виду
Диференціал ентальпії di є елементарне кількість теплоти, яка бере участь в процесі при постійному тиску. Вся теплота в процесі при постійному тиску витрачається на зміну ентальпії:
(5-15)
(5-16)
Ентальпія більше зовнішньої теплоти на величину роботи vdp, яка на рv-діаграмі зображується елементарної майданчиком abed (рис. 5-11). Очевидно, вся пл. ABCD визначається виразом
, яке називається располагаемой, або корисною, роботою.
Зміна ентальпії повністю визначається початковим і кінцевим станом робочого тіла і не залежить від проміжних станів. Зміна ентальпії газу в циклах одно нулю, т. Е.
Оскільки ентальпія є функцією основних параметрів стану, то di є повний диференціал цієї функції при будь-яких незалежних змінних, що характеризують стан газу;
(5-17)
Зміна ентальпії в усіх процесах, що протікають між двома точками А і В, буде однаковим (рис. 5-12).
Фізичний сенс ентальпії буде зрозумілий з розгляду наступного прикладу. На переміщується поршень в циліндрі з 1 кг газу поміщена гиря масою т кг (рис. 5-13). Площа поршня /; внутрішня енергія робочого тіла і. Потенційна енергія гирі дорівнює добутку маси гирі т на висоту S. Так як тиск газу р врівноважується масою гирі, то потенційну енергію її можна виразити інакше:
Твір / S є питома обсяг газу. Звідси
Твір тиску на обсяг є робота, яку треба затратити, щоб ввести газ обсягом v в зовнішнє середовище з тиском р. Таким чином, робота pv є потенційна енергія газу, що залежить від сил, що діють на поршень. Чим більше ці зовнішні сили, тим більше тиск р і тим більше потенційна енергія тиску pv.
Якщо розглядати газ, що знаходиться в циліндрі і поршень з вантажем як одну систему, яку будемо називати розширеною системою, то повна енергія Е цієї системи складається з внутрішньої енергії газу і і потенційної енергії поршня з вантажем, що дорівнює pv:
Звідси видно, що ентальпія i дорівнює енергії розширеної системи. тіла і навколишнього середовища. В цьому і полягає фізичний зміст ентальпії.
Значення ентальпій для парів, газів і газових сумішей наводяться в технічній і довідковій літературі. Користуючись цими даними, можна визначати кількість теплоти, яка бере участь в процесі при постійному тиску. Ентальпія набула великого значення і застосування при розрахунках теплових і холодильних установок і, як параметр стану робочого тіла, значно спрощує теплові розрахунки. Вона дозволяє [застосовувати графічні методи при дослідженні всіляких термодинамічних процесів і циклів.
Ентальпії особливо доцільно користуватися тоді, коли в якості основних параметрів приймають р і Т. Це наочно можна бачити, якщо ентальпію i порівняти з внутрішньою енергією і. При v = const рівняння першого закону термодинаміки dq = = du pdv перетворюється в dqv = du, або qv. u2-u1 а при р = const qp = i3. i1.
Ентальпія ідеального газу, ‘так само як і внутрішня енергія, є функцією температури і не залежить від інших параметрів. Дійсно, для ідеального газу
отже (оскільки обидва доданків залежать тільки від температури), i = f (T).
Тоді за аналогією з внутрішньою енергією матимемо
т. е. в будь-якому процесі зміни стану ідеального газу похідна від зміни ентальпії по температурі буде повною похідною.
Чисельні значення ентальпій ідеальних газів наведені в додатку, табл. XIII.
Дата додавання: 2018-02-15; переглядів: 1423; ЗАМОВИТИ РОБОТУ
Електронний навчальний посібник Москва 2013
Молярна маса суміші n газів
.
Масова частка i-го компонента суміші газу (в частках одиниці або відсотках)
9 клас. Середня молярна маса газової суміші
,
Як знайти молекулярну масу суміші
Ocновние поняття і закони хімії. Атомно-молекулярне вчення
2.10.1. Розрахунок відносних і абсолютних мас атомів і молекул
Відносні маси атомів і молекул визначаються з використанням наведених в таблиці Д.І. Менделєєва величин атомних мас. При цьому, при проведенні розрахунків для навчальних цілей значення атомних мас елементів зазвичай округлюються до цілих чисел (за винятком хлору, атомна маса якого приймається рівною 35,5).
Приклад 1. Відносна атомна маса кальцію Аr (Са) = 40; відносна атомна маса платини Аr (Pt) = 195.
Відносна маса молекули розраховується як сума відносних атомних мас складових дану молекулу атомів з урахуванням кількості їх речовини.
Приклад 2. Відносна молярна маса сірчаної кислоти:
Величини абсолютних мас атомів і молекул знаходяться розподілом маси 1 моль речовини на число Авогадро.
Приклад 3. Визначте масу одного атома кальцію.
Рішення. Атомна маса кальцію становить Аr (Са) = 40 г / моль. Маса одного атома кальцію виявиться рівною:
m (Ca) = Аr (Ca): NA = 40: 6,02 х 10 23 = 6,64 10.23 г.
Приклад 4. Визначте масу однієї молекули сірчаної кислоти.
Рішення. Молярна маса сірчаної кислоти дорівнює Мr (H2SO4) = 98. Маса однієї молекули m (H2SO4) дорівнює:
Відносна густина, об`єм, середня молярна маса суміші газів. Молярна маса та маса. Хімія 8, 9, 10
2.10.2. Розрахунок кількості речовини і обчислення числа атомних і молекулярних частинок за відомими значеннями маси і об’єму
Кількість речовини визначається шляхом ділення його маси, вираженої в грамах, на його атомну (молярна) масу. Кількість речовини, що знаходиться в газоподібному стані при н.у., знаходиться діленням його обсягу на обсяг 1 моль газу (22,4 л).
Приклад 5. Визначте кількість речовини натрію n (Na), що знаходиться в 57,5 г металевого натрію.
Рішення. Відносна атомна маса натрію дорівнює Аr (Na) = 23. Кількість речовини знаходимо діленням маси металевого натрію на його атомну масу:
Приклад 6. Визначте кількість речовини азоту, якщо його обсяг при н.у. становить 5,6 л.
Рішення. Кількість речовини азоту n (N 2) знаходимо діленням його обсягу на обсяг 1 моль газу (22,4 л):
Вебінар 13. Відносна густина газів. Середня морлярна маса суміші речовин. ЗНО-2021 з хімії
Число атомів і молекул в речовині визначається множенням кількості речовини атомів і молекул на число Авогадро.
Приклад 7. Визначте число молекул, що містяться в 1 кг води.
Рішення. Кількість речовини води знаходимо діленням її маси (1000 г) на молярну масу (18 г / моль):
N (Н2О) = 55,5 6,02 х 10 23 = 3,34 × 10 24.
Приклад 8. Визначте число атомів, що містяться в 1 л (н.у.) кисню.
Рішення. Кількість речовини кисню, обсяг якого при нормальних умовах становить 1 л одно:
n (О2) = 1: 22,4 = 4,46 10.2 моль.
Число молекул кисню в 1 л (н.у.) складе:
N (О2) = 4,46 10.2 6,02 х 10 23 = 2,69 × 10 22.
Слід зазначити, що 26,9 х 10 22 молекул міститиметься в 1 л будь-якого газу при н.у. Оскільки молекула кисню двоатомних, число атомів кисню в 1 л буде в 2 рази більше, тобто 5,38 × 10 22.
2.10.3. Розрахунок середньої молярної маси газової суміші і об’ємної частки містяться в ній газів
Середня молярна маса газової суміші розраховується на основі молярних мас складових цю суміш газів і їх об’ємних часток.
Приклад 9. Вважаючи, що (в об’ємних відсотках) азоту, кисню і аргону в повітрі відповідно становить 78, 21 і 1, розрахуйте середню молярну масу повітря.
Мвозд = 0,78 Мr (N2) 0,21 Мr (O2) 0,01 Мr (Ar) = 0,78 280,21 320,01 40 = 21,846,720,40 = 28,96
Приклад 10. Газова суміш містить 12 л NH3, 5 л N2 і 3 л Н2, виміряних при н.у. Розрахувати об’ємні частки газів в цій суміші і її середню молярну масу.
Рішення. Загальний обсяг суміші газів дорівнює V = тисячі двісті п’ятьдесят три = 20 л. Об’ємні частки j газів виявляться рівними:
Середня молярна маса розраховується на основі об’ємних часток складових цю суміш газів і їх молекулярних мас:
М = 0,6 М (NH3) 0,25 M (N2) 0,15 M (H2) = 0,6 170,25 280,15 2 = 17,5.
2.10.4. Розрахунок масової частки хімічного елемента в хімічній сполуці
Масова частка ω хімічного елемента визначається як відношення маси атома даного елемента Х, що міститься в даній масі речовини до маси цієї речовини m. Масова частка. безрозмірна величина. Її виражають в частках від одиниці:
ω (X) = m (X) / m (0 о С і тиску 200 кПа маса 3,0 л газу становить 6,0 г. Визначте молярну масу цього газу.
Рішення. Підставляючи відомі величини в рівняння Клапейрона-Менделєєва отримуємо:
М = mRT / PV = 6,0 8,31 313 / (200 3,0) = 26,0.
Приклад 17. При згорянні 5,6 л (н.у.) вуглеводню отримано 44,0 г вуглекислого газу і 22,5 г води. Відносна щільність вуглеводню по кисню дорівнює 1,8125. Визначте справжню хімічну формулу вуглеводню.
Рішення. Рівняння реакції згоряння вуглеводню можна представити таким чином:
Кількість вуглеводню становить 5,6: 22,4 = 0,25 моль. В результаті реакції утворюється 1 моль вуглекислого газу і 1,25 моль води, яка містить 2,5 моль атомів водню. При спалюванні вуглеводню кількістю речовини 1 моль виходить 4 моль вуглекислого газу і 5 моль води. Таким чином, 1 моль вуглеводню містить 4 моль атомів вуглецю і 10 моль атомів водню, тобто хімічна формула вуглеводню С4Н10. Молярна маса цього вуглеводню дорівнює М = 4 1210 = 58. Його відносна щільність по кисню D = 58: 32 = 1,8125 відповідає величині, наведеної в умові завдання, що підтверджує правильність знайденої хімічної формули.
Якщо ідеальні гази знаходяться в сполучених балонах, розділених краном, то при відкритті крана гази в балонах змішуються між собою і кожен з них заповнює обсяг обох балонів.
Для ідеального газу (або двох різних газів), що знаходиться в сполучених балонах. при відкритті крана деякі параметри стають однаковими:
- тиск газу (або суміші газів) після відкриття крана зрівнюється:
- газ (або суміш газів) після відкриття крана займає весь наданий йому об’єм, тобто обсяг обох судин:
де V 1. обсяг першого балона; V 2. об’єм другого балона;
- температура газу (або суміші газів) після відкриття крана зрівнюється:
- щільність газу ρ та його концентрація n в обох балонах стають однаковими:
Якщо балони мають однаковий обсяг. то маси газу (або суміші газів) в кожному балоні після відкриття крана стають однаковими:
де m ‘1. маса газу (або суміші газів) в першому балоні після відкриття крана; m ‘2. маса газу (або суміші газів) у другому балоні після відкриття крана; m ‘- маса газу (або суміші газів) в кожному балоні після відкриття крана; m 1. маса газу в першому балоні до відкриття крана; m 2. маса газу в другому балоні до відкриття крана.
Маса газу, який перейшов з однієї судини в іншій в результаті відкриття крана, визначається наступними виразами:
- зміна маси газу в першому балоні
Δ m 1 = | m ‘1. m 1 | = | m 1 m 2 2. m 1 | = | m 2. m 1 | 2;
- зміна маси газу в другому балоні
Δ m 2 = | m ‘2. m 2 | = | m 1 m 2 2. m 2 | = | m 1. m 2 | 2.
Зміни маси газу (або суміші газів) в обох балонах однакові:
тобто скільки газу пішло з балона з більшою масою газу. стільки ж газу прийшло в балон з меншою масою.
Якщо балони мають однаковий обсяг. то кількості газу (або суміші газів) в кожному балоні після відкриття крана стають однаковими:
де ν ‘1. кількість газу (або суміші газів) в першому балоні після відкриття крана; ν ‘2. кількість газу (або суміші газів) у другому балоні після відкриття крана; ν ‘- кількість газу (або суміші газів) в кожному балоні після відкриття крана; ν 1. кількість газу в першому балоні до відкриття крана; ν 2. кількість газу в другому балоні до відкриття крана.
Кількість газу, який перейшов з однієї судини в іншій в результаті відкриття крана, визначається наступними виразами:
- зміна кількості газу в першому балоні
Δ ν 1 = | ν ‘1. ν 1 | = | ν 1 ν 2 2. ν 1 | = | ν 2. ν 1 | 2;
- зміна кількості газу в другому балоні
Δ ν 2 = | ν ‘2. ν 2 | = | ν 1 ν 2 2. ν 2 | = | ν 1. ν 2 | 2.
Зміни кількості газу (або суміші газів) в обох балонах однакові:
тобто скільки газу пішло з балона з великою кількістю газу. стільки ж газу прийшло в балон з меншою кількістю.
Для ідеального газу (або двох різних газів), що знаходиться в сполучених балонах, при відкритті крана тиск стає однаковим:
і визначається за законом Дальтона (для суміші газів).
де p 1. p 2. парціальні тиску компонентів суміші.
Парціальні тиску компонентів суміші можуть бути розраховані наступним чином:
- за допомогою рівняння Менделєєва. Клапейрона; тоді тиск визначається формулою
де ν 1. кількість речовини першого компонента суміші; ν 2. кількість речовини другого компонента суміші; R. універсальна газова постійна, R ≈ 8,31 Дж / (моль ⋅ К); T. температура суміші; V 1. обсяг першого балона; V 2. об’єм другого балона;
- за допомогою основного рівняння молекулярно-кінетичної теорії; тоді тиск визначається формулою
де N 1. кількість молекул першого компонента суміші; N 2. кількість молекул другого компонента суміші; k. постійна Больцмана, k = 1,38 ⋅ 10.23 Дж / К.
Приклад 26. Визначити середню молярну масу суміші газів, що складається з 3,0 кг водню, 1,0 кг гелію і 8,0 кг кисню. Молярні маси водню, гелію і кисню рівні 2,0, 4,0 і 32 г / моль відповідно.
Рішення. Середня молярна маса суміші визначається формулою
де m. маса суміші; ν. кількість речовини в суміші.
де m 1. маса водню; m 2. маса гелію; m 3. маса кисню.
де ν 1. кількість водню в суміші, ν 1 = m 1 / M 1; M 1. молярна маса водню; ν 2. кількість гелію в суміші, ν 2 = m 2 / M 2; M 2. молярна маса гелію; ν 3. кількість кисню в суміші, ν 3 = m 3 / M 3; M 3. молярна маса кисню.
Підстановка виразів для маси і кількості речовини в вихідну формулу дає
Приклад 27. Щільність суміші газів, що складається з гелію і водню, при тиску 3,50 МПа і температурі 300 К, дорівнює 4,50 кг / м 3. Визначити масу гелію в 4,00 м 3 суміші. Молярні маси водню і гелію рівні 0,002 і 0,004 кг / моль відповідно.
Рішення. Щоб знайти масу гелію m 2 в зазначеному обсязі, необхідно визначити щільність гелію в суміші:
де ρ 2. щільність гелію; V. об’єм суміші газів.
Щільність суміші визначається як сума щільності водню і гелію:
Однак записана формула містить дві невідомі величини. щільності водню і гелію. Для визначення зазначених величин потрібно ще одне рівняння, в яке входять щільності водню і гелію.
Запишемо закон Дальтона для тиску суміші газів:
де p 1. тиск водню; p 2. тиск гелію.
Для визначення тисків газів запишемо рівняння стану в такій формі:
де R. універсальна газова постійна, R ≈ 8,31 Дж / (моль ⋅ К); T. температура суміші; M 1. молярна маса водню; M 2. молярна маса гелію.
Підстановка виразів для тисків водню і гелію в закон Дальтона дає
Отримано ще одне рівняння з двома невідомими величинами. щільністю водню і щільністю гелію.
Формули для розрахунку щільності і тиску суміші утворюють систему рівнянь:
ρ = ρ 1 ρ 2. p = ρ 1 R T M 1 ρ 2 R T M 2 ,
яку потрібно вирішити щодо щільності гелію.
Для цього висловимо щільності водню з першого і другого рівнянь
ρ 1 = ρ. ρ 2. ρ 1 = M 1 R T (p. ρ 2 R T M 2)
Підставами отриманий вираз в формулу для обчислення маси гелію
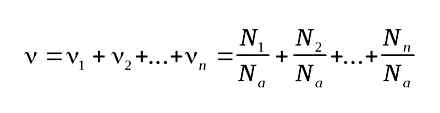
m 2 = 0,004 ⋅ 4,00 0,004. 0,002 (4,50. 3,50 ⋅ 10 6 0,002 8,31 ⋅ 300) ≈ 13,6 кг.
Маса гелію в зазначеному обсязі суміші становить 13,6 кг.
Умова: Зробити розрахунок термодинамічних параметрів газової суміші, що здійснює ізобарна розширення до обсягу V2. якщо відомі початкова температура t1 = 50ºC, початковий тиск р1 = 3 МПа і маса МСМ = 4 кг. Визначити газову сталу і уявну молекулярну масу, початковий обсяг V1. основні параметри в кінцевому стані, зміна внутрішньої енергії, ентальпії, ентропії, теплоту і роботу розширення в процесі 1-2. При визначенні молярної маси і газової постійної звернути увагу на спосіб завдання суміші. Теплоємність компонентів суміші розрахувати з використанням закону Майера. Для розрахунку параметрів стану використовувати рівняння стану ідеальних газів Правильність обчислення енергетичних параметрів контролювати по виконанню 1 закону термодинаміки. Склад газової суміші за обсягом: Cp = 96, 06%; C2p = 2, 0%; C3H8 = 0, 3%; C4h20 = 0, 01%; C5h22 = 0, 1%; N2 = 1, 0%; CO2 = 0, 1%; h3O = 0, 43%; ρ = V2 / V1 = 3, 5.
Умова: По заданому складу газової суміші розрахувати: гадану (середню) молекулярну масу суміші, газову постійну, щільність, середню масову теплоємність суміші при постійному тиску в межах температур від t1 = 100ºC до t2 = 835ºC, кількість тепла, отримане газовою сумішшю при її нагріванні від t1 = 100ºC до t2 = 835ºC. Масова частка азоту. 0,6; води. 0,2; вуглекислого газу. 0,2. Об’єм суміші V = 300 м3, тиск. р1 = 3 бар.
Умова: Зробити розрахунок термодинамічних параметрів газової суміші, що здійснює ізобарна розширення до обсягу V2. якщо відомі початкова температура t1 = 70ºC, початковий тиск р1 = 5 МПа і маса МСМ = 2 кг. Визначити газову сталу і уявну молекулярну масу, початковий обсяг V1. основні параметри в кінцевому стані, зміна внутрішньої енергії, ентальпії, ентропії, теплоту і роботу розширення в процесі 1-2.- При визначенні молярної маси і газової постійної звернути увагу на спосіб завдання суміші Теплоємність компонентів суміші розрахувати з використанням закону Майера.- Для розрахунку параметрів стану використовувати рівняння стану ідеальних газов.- Правильність обчислення енергетичних параметрів контролювати по виконанню 1 закону термодинаміки. Склад газової суміші за обсягом: Cp = 94, 2%; C2p = 3, 0%; C3H8 = 0, 9%; C4h20 = 0, 17%; C5h22 = 0, 22%; N2 = 0, 9%; CO2 = 0, 3%; h3O = 0, 31%; ρ = V2 / V1 = 3, 5.
ВСТУП В ЗАГАЛЬНУ хімію
Електронний навчальний посібник Москва 2013
Як знайти середню молярну масу суміші газів
V. Визначення середньої молярної маси суміші газів
Формули і поняття, які використовуються:
де М (суміші). середня молярна маса суміші газів,
М (А), М (Б), М (В). молярні маси компонентів суміші А, Б і В,
χ (А), χ (B), χ (В). молярний частки компонентів суміші А, Б і В,
φ (А), φ (B), φ (В). об’ємні частки компонентів суміші А, Б і В,
М r (пов.). відносна молекулярна маса повітря.
Завдання 23. Визначте молярну масу суміші, в якій об’ємні частки метану і бутану відповідно становлять 85 і 15%.
Молярна маса суміші. це маса всіх її складових, взятих в сумарній кількості речовини суміші 1 моль (М (СН 4) = 16 г / моль, М (С4Н10) = 58 г / моль). Обчислити середню молярну масу суміші можна за формулою:
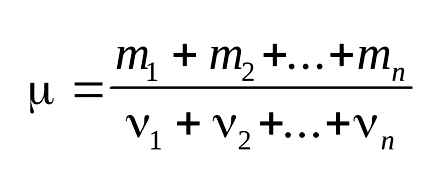
Завдання 24. Визначте щільність газової суміші з азотом, в якій об’ємні частки карбон (І V) оксиду, сульфур (І V) оксиду і карбон (II) оксиду відповідно становлять 35,25 і 40%.
Обчислимо молярну масу суміші (М (С O 2) = 44 г / моль, M (SO 2) = 64 г / моль, М (СО) = 28 г / моль):
Обчислимо відносну щільність суміші з азотом:
Завдання 25. Щільність суміші ацетилену і бутеніл за гелієм дорівнює 11. Визначте об’ємну частку ацетилену в суміші.
За формулою визначимо молярніймасі суміші (М (Не) = 4 г / моль):
Припустимо, що ми маємо 1 моль суміші. У ній міститься х моль С2Н2, тоді відповідно
Запишемо вираз для обчислення середньої молярної маси газової суміші:
Підставами всі відомі дані: М (С2Н2) = 26 г / моль, М (С4Н8) = 56 г / моль:
Отже, 1 моль суміші містить 0,4 моль С2Н2. Обчислимо Мольн частку χ (С2Н2):
Для газів φ (Х) = χ (Х). Отже, φ (С2Н4) = 40%.
.5. Суміші газів
Виникає природне запитання: якими рівняннями описуються суміші ідеальних газів? Адже з чистими газами нам рідко доводиться зустрічатися в природі. Наприклад, наша природне середовище проживання. повітря. складається з азоту N2 (78,08%), кисню O2 (20,95%), інертних газів (0,94%), вуглекислого газу СО2 (0,03%).
Нехай в деякому обсязі V при деякій температурі Т міститься суміш газів (які ми будемо нумероватьіндексом i). Роль кожного компонента суміші будемо характеризувати масовою часткою:
де Mi. маса i-го компонента. Наше завдання. написати рівняння, подібне рівняння Клапейрона. Менделєєва, і розібратися з ефективним числом ступенів свободи суміші, де можуть міститися і одноатомні, і багатоатомні молекули.
Перш за все, зауважимо, що ми розглядаємо ідеальні гази. Молекули не взаємодіють один з одним, і тому кожен компонент не заважає будь-якій іншій «жити» в тому ж загальному посудині. Різні гази в посудині, в силу їх передбачуваної ідеальності, просто «не помічають» один одного. Тому для кожного з компонентів справедливо одне і те ж рівняння Клапейрона. Менделєєва:
де ni. число молей речовини в i.м компоненті. Повне число n молей в суміші дорівнює сумі числа молей ni в кожному з компонентів:
Аналогічно, повна маса суміші дорівнює сумі мас кожного з компонентів
і природно визначити молярну масу суміші m як масу одного моля суміші:
Введемо величину, яка називається парціальним тиском.
Парціальний тиск pi. це тиск, який чиниться i-м компонентом газової суміші.
Має місце закон Дальтона для газової суміші:
Повний тиск газової суміші дорівнює сумі всіх парціальних тисків
Молярну масу суміші газів знайдемо за формулою
(5)
де 1 і 2. число молей гелію і водню відповідно. Число молей газів визначимо за формулами:
(6)
(7)
(8)
Підставляючи числові значення в формули (4) і (8), отримуємо:
відповідь:p = 2493 кПа, = 3 10.3 кг / моль.
завдання 8. Чому рівні середні кінетичні енергії поступального і обертального руху молекул, що містяться в 2 кг водню при температурі 400 К?
Рішення. Вважаємо водень ідеальним газом. Молекула водню. двухатомная, зв’язок між атомами вважаємо жорсткою. Тоді число ступенів свободи молекули водню дорівнює 5. У середньому на одну ступінь свободи доводиться енергія =kТ / 2 , де k-постійна Больцмана; T-термодинамічна температура. Поступального руху приписується три (i= 3), а обертального дві (i = 2) ступеня свободи. Енергія однієї молекули
Число молекул, що містяться в масі газу, так само
де v. число молей; NA. постійна Авогадро.
Тоді середня кінетична енергія поступального руху молекул водню
(1)
де R = k NА – молярна газова стала.
Середня кінетична енергія вращательногодвіженія молекул водню
(2)
Підставляючи числові значення в формули (1) і (2), маємо
відповідь: = 4986кДж, = 2324кДж.
завдання 9. Визначити середню довжину вільного пробігу молекул і число зіткнень за 1 с, що відбуваються між усіма молекулами кисню, що знаходиться в посудині ємністю 2 л при температурі 27 ° С і тиску 100 кПа.
Рішення. Середня довжина вільного пробігу молекул кисню обчислюється за формулою
(1)
де d. ефективний діаметр молекули кисню; п. число молекул в одиниці об’єму, яке можна визначити з рівняння
(3)
число зіткненьZ, що відбуваються між усіма молекулами за 1 с, одно
(4)
де N. число молекул кисню в посудині об’ємом 2 10.3 м 3;
Середнє число зіткнень молекули за 1 з одно
(6)
де. середня арифметична швидкість молекули
(7)
Підставляючи в (4) вирази (5), (6) і (7), знаходимо
відповідь: Z = 9 10 28 с- 1. =3,56 10.8 м.
завдання 10. Визначити коефіцієнти дифузії і внутрішнього тертя азоту, що знаходиться при температурі Т = 300 К і тиску 10 5 Па.
Рішення. Коефіцієнт дифузії визначається за формулою
(1)
де. середня арифметична швидкість молекул, що дорівнює
(2)
Для знаходження скористаємося формулою з рішення прикладу 4
(3)
(4)
(5)
де р. щільність газу при температурі 300 К і тиску 10 5 Па. для знаходження р скористаємося рівнянням стану ідеального газу. Запишемо його для двох станів азоту. при нормальних умовах те= 273 К, р= 1,01 10 5 Па і в умовах завдання:
(6)
,
. (7)
Коефіцієнт внутрішнього тертя газу може бути виражений через коефіцієнт дифузії (див. Формули (1) і (5)):
Підставляючи числові значення в (4) і (8), отримаємо
відповідь: D = 4,7 10.5 м 2 / с,
завдання 11. Обсяг аргону, що знаходиться при тиску 80кПа, збільшився від 1 до 2 л. На скільки зміниться внутрішня енергія газу, якщо розширення вироблялося: а) ізобарно, б) адіабатно.
Рішення. Застосуємо перший закон термодинаміки. Згідно з цим законом, кількість теплоти Q, передане системі, витрачається на збільшення внутрішньої енергії U і на зовнішню механічну роботу А:
Q = UА (1)
Величину U можна визначити, знаючи масу газу m, питому теплоємність при постійному обсязі СV і зміна температури Т:
(2)
Однак зручніше зміна внутрішньої енергії U визначати через молярну теплоємність Cv, яка може бути виражена через число ступенів свободи:
(3)
(4)
Зміна внутрішньої енергії залежить від характеру процесу, при якому йде розширення газу. При изобарном розширенні газу, згідно з першим законом термодинаміки, частина кількості теплоти йде на зміну внутрішньої енергії U, яка виражається формулою (4) Знайти U для аргону за формулою (4) не можна, так як маса газу і температура в умові завдання не дані. Тому необхідно провести перетворення формули (4).
Запишемо рівняння Клапейрона. Менделєєва для початкового і кінцевого станів газу:
(5)
(6)
Це рівняння є розрахунковим для визначення при изобарном розширенні.
При адіабатні розширенні газу теплообміну з зовнішнім середовищем не відбувається, тому Q= 0. Рівняння (1) запишеться у вигляді
(7)
(8)
Це співвідношення встановлює, що робота розширення газу може бути проведена тільки за рахунок зменшення внутрішньої енергії газу (знак мінус перед):
Формула роботи для адиабатного процесу має вигляд
(9)
де. показник ступеня адіабати, рівний відношенню теплоємності:
Для аргону. одноатомного газу (i= 3). маємо = 1,67.
Знаходимо зміна внутрішньої енергії при адіабатні процесі для аргону, враховуючи формули (8) і (9):
(10)
Для визначення роботи розширення аргону формулу (10) слід перетворити, враховуючи при цьому параметри, дані в умові задачі. Застосувавши рівняння Клапейрона. Менделєєва для даного випадку. отримаємо вираз для підрахунку зміни внутрішньої енергії:
(11)
Підставляючи числові значення в (6) і (11), маємо:
відповідь:
завдання 12.Заряд 15 ∙ 10.9 Кл рівномірно розподілений по тонкому кільцю радіусом 0,2 м. Знайдіть напруженість електричного поля в точці, що знаходиться на осі кільця на відстані 15 см від його центру.
Рішення. Розділимо кільце на однакові нескінченно малі ділянки dl. Заряд кожної ділянки dq можна вважати точковим.
Напруженість електричного поля dE. створюваного в точці А на осі кільця зарядом dq, дорівнює:
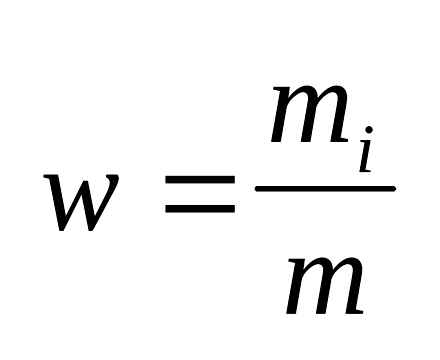
(1)
де (2)
Повна напруженість поля Е в точці А, створювана зарядом q, згідно з принципом суперпозиції дорівнює векторній сумі напруженостей dEi полів, створюваних усіма точковими зарядами:
вектор dE розкладемо на складові: вектор dE1 (Спрямований уздовж осі кільця) і вектор dE2 (Паралельний площині кільця).
тоді
Для кожної пари зарядів dq і dq /. розташованих симетрично щодо центру кільця, dE2 і dE / 2 в сумі дадуть нуль, і значить
складові dE1 для всіх елементів спрямовані однаково уздовж кільця, тому повна напруженість в точці, що лежить на осі кільця, також спрямована уздовж осі.
Модуль повної напруженості знайдемо інтегруванням:
(3)
де α-кут між вектором dE і віссю кільця;
(4)
Використовуючи вирази (1), (2) і (4), для E отримуємо:
завдання 13. Заряд переноситься в повітрі з точки, що знаходиться на відстані 1 м від нескінченно довгої рівномірно зарядженої нитки, в точку на відстані 10 см від неї. Визначити роботу, що здійснюються проти сил поля, якщо лінійна щільність заряду нитки 1 мкКл / м. Яка робота здійснюється на останніх 10 см шляху?
Рішення.Робота зовнішньої сили по переміщенню заряду q з точки поля з потенціалом φi в точку з потенціалом φ0 дорівнює
(1)
Нескінченна рівномірно заряджена нитка з лінійною щільністю заряду τ створює аксіально-симетричне поле напруженістю.
Напруженість і потенціал цього поля пов’язані співвідношенням
, звідки.
Різниця потенціалів точок поля на відстані ri і r0 від нитки
(2)
Підставляючи в формулу (1) знайдене вираз для різниці потенціалів з (2), визначимо роботу, що здійснюються зовнішніми силами по переміщенню заряду з точки, що знаходиться на відстані 1 м, до точки, розташованої на відстані 0,1 м від нитки:
відповідь: A1= 4,1 ∙ 10.5 (Дж).
завдання 14. Сила струму в провіднику опором 20 Ом наростає протягом часу 2 с по лінійному закону від 0 до 6 А. Визначити теплоту Q1, що виділилася в цьому провіднику за першу секунду, і Q2. за другу, а також визначити ставлення Q2 / Q1.
Рішення.Закон Джоуля-Ленца в вигляді справедливий для постійного струму. Якщо ж сила струму в провіднику змінюється, то зазначений закон справедливий для нескінченно малого інтервалу часу і записується у вигляді
(1)
Тут сила струму є деякою функцією часу.
, (2)
де k. коефіцієнт пропорційності, що характеризує швидкість зміни сили струму:
(3)
Для визначення теплоти, що виділилася за кінцевий інтервал часу Δt, вираз (3) треба проінтегрувати в межах від t1 до t2:
,
тобто за другу секунду виділиться теплоти в сім разів більше, ніж за першу.
завдання 15. Електричне коло складається з двох гальванічно; елементів, трьох опорів і гальванометра. У цьому ланцюзі R1 = 100 Ом, R2 = 50 Ом, R3 = 20 Ом, е.р.с. елемента ε1 = 2 В. гальванометр реєструє ток I3 = 50 мА, що йде в напрямку стрілки. визначити е.р.с. другого елемента. Опором гальванометра і внутрішнім опором елементів знехтувати.
вказівка. Для розрахунку розгалужених ланцюгів застосовуються закони Кирхгофа.
Перший закон Кірхгофа. Алгебраїчна сума сил струмів, що сходяться у вузлі, дорівнює нулю, тобто
Другий закон Кірхгофа. У будь-якому замкнутому контурі алгебраїчна сума напруг на окремих ділянках кола дорівнює алгебраїчній сумі е.р.с., що зустрічаються в контурі.
На підставі цих законів можна скласти рівняння, необхідні для визначення шуканих величин (сил струмів, опорів і Е.Д.С.). Застосовуючи закони Кірхгофа, слід дотримуватися таких правил:
Перед складанням рівнянь довільно вибрати: а) напрямки струмів (якщо вони не задані по умові завдання) і вказати їх стрілками на кресленні; б) напрямок обходу контурів.
При складанні рівнянь за першим законом Кірхгофа вважати струми, які підходять до вузла, позитивними; струми, що відходять від вузла, негативними. Число рівнянь, що складаються за першим законом Кірхгофа, має бути на одиницю менше числа вузлів, що містяться в ланцюзі.
При складанні рівнянь за другим законом Кірхгофа треба вважати, що: а) падіння напруги на ділянці кола (т. Е. Твір Ir) Входить в рівняння зі знаком плюс, якщо напрямок струму в даній ділянці збігається з вибраним напрямком обходу контуру; в іншому випадку твір Ir входить в рівняння зі знаком мінус; б) Е.Д.С. входить в рівняння зі знаком плюс, якщо вона підвищує потенціал у напрямку обходу контуру, т. е. якщо при обході доводиться йти від мінуса до плюса всередині джерела струму; в іншому випадку е.р.с. входить в рівняння зі знаком мінус.
Число незалежних рівнянь, які можуть бути складені за другим законом Кірхгофа, повинна бути меншою ніж замкнутих контурів, наявних в ланцюзі. Для складання рівнянь перший контур можна вибирати довільно. Усі наступні контури слід вибирати таким чином, щоб в кожен новий контур входила хоча б одна гілка ланцюга, не брала участь ні в одному з раніше використаних контурів. Якщо при вирішенні рівнянь, складених зазначеним вище способом, отримані негативні значення сили струму або опору, то це означає, що струм через дане опір в дійсності тече в напрямку, протилежному довільно обраного.
Рішення. Виберемо напрямки струмів, як вони показані на малюнку, і домовимося обходити контури за годинниковою стрілкою.
За першим законом Кірхгофа для вузла F маємо: (1)
За другим законом Кірхгофа маємо для контуру ABCDFA:
,
або після множення обох частин рівності на.1
(2)
(3)
Після підстановки числових значень в формули (1), (2) і (3) отримаємо:
Цю систему з трьома невідомими можна вирішити звичайними прийомами алгебри, але так як за умовою завдання потрібно визначити тільки одне невідоме ε2 з трьох, то скористаємося методом визначників.
Складемо і обчислимо визначник Δ системи:
Розділивши визначник Δε2 на визначник Δ, знайдемо числове значення ε2:
завдання 16. Плоский квадратний контур зі стороною 10 см, по якому тече струм силою 100 А, вільно встановився в однорідному магнітному полі індукції 1Тл. Визначити роботу, що здійснюються зовнішніми силами при повороті контуру відносно осі, що проходить через середину його протилежних сторін, на кут 90 0. При повороті контуру сила струму в ньому підтримується незмінною.
Рішення. Як відомо, на контур зі струмом в магнітному полі діє момент сили: (1) где.магнітний момент контуру;.магнітная індукція;.Кут між векторами і.
За умовою завдання в початковому положенні контур вільно встановився в магнітному полі. При цьому момент сил дорівнює нулю М = 0, а значить, = 0, тобто вектори і сонаправлени. Якщо зовнішні сили виведуть контур з положення рівноваги, то що виник момент сил буде прагнути повернути контур в початкове положення. Проти цього моменту і буде відбуватися робота зовнішніми силами. Так як момент сил змінний (залежить від кута повороту), то для підрахунку роботи формулу роботи в диференціальної формі. З огляду на формулу (1), отримуємо. Взявши інтеграл від цього виразу, знайдемо роботу при повороті на кінцевий кут:
Робота при повороті на кут = 90 0 :
(3)
Підставами в отриману формулу числові значення, отримаємо: А = 1Дж. Завдання можна вирішити і іншим способом. Робота зовнішніх сил по переміщенню контура зі струмом в магнітному полі дорівнює добутку сили струму в контурі на зміну магнітного потоку через контур:
,
де Ф1.магнітний потік, що пронизує контур до переміщення;
Якщо = 90 0. то Ф1 = BS, Ф1 = 0.
Отже. що збігається з формулою (3).
завдання 17. Електрон, пройшовши прискорює різниця потенціалів 400 В, потрапив в однорідне магнітне поле напруженістю 1 кА / м. Визначити радіус кривизни траєкторії і частоту обертання електрона в магнітному полі. Вектор швидкості перпендикулярний лініям поля.
Рішення. Радіус кривизни траєкторії електрона визначимо, виходячи з таких міркувань: на рухомий в магнітному полі, діє сила Лоренца.
Сила Лоренца перпендикулярна вектору швидкості, отже, повідомляє електрону нормальне прискорення. За другим законом Ньютона. де. нормальне прискорення, або (1)
де q– заряд, в нашому випадку елементарний заряд;.скорость електрона, В- магнітна індукція, m- маса електрона, R-радіус кривизни траєкторії, α. кут між векторами і B (в даному випадку В і. sin α = 1).
(2)
Твір, добуток. що входять в рівність (2), висловимо через кінетичну енергію
.
Але кінетична енергія електрона, що пройшов прискорює різниця потенціалів, можна визначити. Підставивши вираз T в формулу (3), отримаємо
(3)
Магнітна індукція може бути виражена через напруженість магнітного поля в вакуумі:
(4)
Підставивши вирази (3) і (4) в формулу (2), отримаємо
Провівши обчислення, отримаємо: R = 5,37 ∙ 10.2 м.
Для визначення частоти звернення скористаємося формулою, що зв’язує частоту зі швидкістю і радіусом:
(5)
Підставивши в формулу (5) вираз (2), отримуємо
або
Провівши обчислення, отримуємо: n=3,52 ∙ 10 7 с.1.
відповідь: R = 5,37 ∙ 10.2 м, n = 3,52 ∙ 10 7 с.1.
завдання 18. В однорідному магнітному полі індукції 0,1 Тл рівномірно з частотою 10 с.1 обертається рамка, яка містить 1000 витків, які щільно прилягають одна до одної. Площа рамки дорівнює 150 см 2. визначити миттєве значення ЕРС індукції, відповідні куту повороту рамки, рівному 30 0
Рішення. Миттєве значення ЕРС індукції визначається основним рівнянням електромагнітної індукції Фарадея-Максвелла:
(1)
Потокосцепление пов’язано з магнітним потоком і числом витків, які щільно прилягають одна до одної, співвідношенням
(2)
Підставляючи вираз (2) у формулу (1), отримуємо
При обертанні рамки магнітний потік Ф, що пронизує рамку в момент часу t, визначається співвідношенням. де B-магнітна індукція, S. площа рамки, ω. кругова (або циклічна) частота.
Підставивши в формулу (2) вираз Ф і продифференцировав отриманий вираз по часу, знайдемо миттєве значення ЕРС індукції:
(3)
кругова частота ω пов’язана з частотою обертання n співвідношенням
Підставляючи вираз частоти в формулу (3) і замінивши ωt на φ, отримаємо
.
Провівши обчислення, отримаємо: =47,1 В.
відповідь: =47,1 В.
завдання 19. На щілину шириною 0,1 мм нормально падає паралельний пучок світла від монохроматичного джерела (l = 0,6мкм). визначити ширину l центрального максимуму в дифракційної картині, яка проектується за допомогою лінзи, що знаходиться безпосередньо за щілиною, на екран, віддалений від лінзи на відстані L = 1м.
Рішення. Центральний максимум інтенсивності світла займає область між найближчими від нього праворуч і ліворуч мінімумами інтенсивності. Тому ширину центрального максимуму інтенсивності приймемо рівної відстані між цими двома мінімумі інтенсивності (див. Рис.).
Мінімуми інтенсивності світла при дифракції від однієї щілини спостерігаються під кутами j, певними умовою
(1)
де k. порядок min. у нашому випадку k = 1. Відстань між 2-ма мінімумами на екрані визначимо безпосередньо за кресленням:
При малих кутах. тоді (2).
Висловимо sinj з формули (1) і підставимо його в рівність (2):
(3)
Провівши обчислення за формулою (3), отримаємо: l = 1,2 см.
відповідь: l = 1,2 см.
завдання 20. Пучок природного світла падає на поліровану поверхню скління пластини, зануреної в рідину. Відбитий від пластини пучок світла становить кут j = 97 ° з падаючим пучком (див. Рис.) Визначити показник заломлення n1 рідини, якщо відбите світло повністю поляризований.
Рішення. Відповідно до закону Брюстера світло, відбите від діелектрика, повністю поляризований в тому випадку, якщо тангенс кута падіння. де n2,1– відносний показник заломлення другого середовища / скла / щодо першої / рідини /, тобто
За умовою завдання, відбитий промінь повернуть на кут j щодо падаючого променя.
Так як кут падіння дорівнює куту відбиття, то і, отже, звідки.
завдання 21. Довжина хвилі, на яку припадає максимум енергії в спектрі випромінювання абсолютно чорного тіла λ0 = 0,58мкм. Визначити енергетичну світимість (ізлучателность) Re поверхні тіла.
Рішення. енергетична світність Re абсолютно чорного тіла відповідно до закону Стефана. Больцмана пропорційна четвертого ступеня термодинамічної температури і виражається формулою
(1)
де σ.постійна Стефана. Больцмана; Т. термодинамічна температура.
температуру Т можна виразити за допомогою закону зміщення Віна:
(2)
де Ь. постійна закону зміщення Віна. Використовуючи формули (2) і (1), отримуємо
(3)
відповідь: Re = 35,4 МВт / м 2.
завдання 22.Визначити червону межу l0 фотоефекту для металу, якщо при опроміненні його поверхні фіолетовим світлом довжиною хвилі l максимальна швидкість υmax фотоелектронів дорівнює 0,65 Мм / c.
Рішення. При опроміненні світлом з l0, відповідної червоною кордоні фотоефекту кінетична енергія фотоелектронів дорівнює. Рівняння Ейнштейна для фотоефекту
(1)
У разі червоною кордону і ,
звідси
Робота виходу: (2).
Частота падаючого світла: (3).
Тоді з урахуванням (2), (3): (4).
Для визначення червоною кордону фотоефекту підставимо значення в формулу (4) і обчислимо: l0 = 0,65мкм.
завдання 23. Обчислити дефект маси ядра ізотопу неону.
Рішення. Дефект маси ядра дорівнює
З символічного запису елемента неону слід, що А = 20, Z = 10.
mp = 1,6724 × 10.27 дог, mn = 1,6748 × 10.27 дог, MЯ = 33,1888×10 27 дог.
Dm = 10 × (1,6724 × 10.27 1,6748 × 10.27). 33,1888 × 10.27) дог =2,832 × 10.28 дог.
відповідь: Dm=2,832 × 10.28 дог.
завдання 24. Визначити період напіврозпаду радону, якщо за 1 добу з 1 млн. Атомів розпадається 175 000 атомів.
Рішення. Період напіврозпаду радону
Постійну радіоактивного розпаду l знайдемо із співвідношення DN = N0 (1-e. L t), звідки
.
Підставивши цей вираз в першу формулу, отримаємо:
; Т »3,3 × 10 5 с.
завдання 25.В результаті захоплення a-частинки ядром ізотопу азоту утворюються невідомий елемент і протон. Написати реакцію і визначити невідомий елемент.
Рішення. Запишемо ядерну реакцію:
.
Так як суми масових чисел і зарядів в правій і лівій частинах вираження повинні бути рівними, то
Отже, отриманий елемент символічно можна записати у вигляді. Ізтабліци Менделєєва знайдемо, що це ізотоп кисню.
відповідь:.